A-level数学考试：什么是三角函数

 

What is Trigonometry？

本文为全英叙述，可以充分引领你了解三角函数的前世今生，来龙去脉。在本文结尾处，附上三张三角函数公式表，帮助你自如地应付A level数学考试

Trigonometry is a branch of mathematics that studies relationships between the sides and angles of triangles. Trigonometry is found all throughout geometry, as every straight-sided shape may be broken into as a collection of triangles. Further still, trigonometry has astoundingly intricate relationships to other branches of mathematics, in particular complex numbers, infinite series, logarithms and calculus. 

The word trigonometry is a 16th-century Latin derivative from the Greek words for triangle (trigōnon) and measure (metron). Though the field emerged in Greece during the third century B.C., some of the most important contributions (such as the sine function) came from India in the fifth century A.D. Because early trigonometric works of Ancient Greece have been lost, it is not known whether Indian scholars developed trigonometry independently or after Greek influence. According to Victor Katz in “A History of Mathematics 3rd Edition)” (Pearson, 2008), trigonometry developed primarily from the needs of Greek and Indian astronomers.

An example: Height of a sailboat mast

Suppose you need to know the height of a sailboat mast, but are unable to climb it to measure. If the mast is perpendicular to the deck and top of the mast is rigged to the deck, then the mast, deck and rigging rope form a right triangle. If we know how far the rope is rigged from the mast, and the slant at which the rope meets the deck, then all we need to determine the mast’s height is trigonometry.

For this demonstration, we need to examine a couple ways of describing “slant.” First is slope, which is a ratio that compares how many units a line increases vertically (its rise) compared to how many units it increases horizontally (its run). Slope is therefore calculated as rise divided by run. Suppose we measure the rigging point as 30 feet (9.1 meters) from the base of the mast (the run). By multiplying the run by the slope, we would get the rise — the mast height. Unfortunately, we don’t know the slope. We can, however, find the angle of the rigging rope, and use it to find the slope. An angle is some portion of a full circle, which is defined as having 360 degrees. This is easily measured with a protractor. Let’s suppose the angle between the rigging rope and the deck is 71/360 of a circle, or 71 degrees.

We want the slope, but all we have is the angle. What we need is a relationship that relates the two. This relationship is known as the “tangent function,” written as tan(x). The tangent of an angle gives its slope. For our demo, the equation is:  tan(71°) = 2.90. (We'll explain how we got that answer later.)

This means the slope of our rigging rope is 2.90. Since the rigging point is 30 feet from the base of the mast, the mast must be 2.90 × 30 feet, or 87 feet tall. (It works the same in the metric system: 2.90 x 9.1 meters = 26.4 meters.)

Sine, cosine and tangent

Depending on what is known about various side lengths and angles of a right triangle, there are two other trigonometric functions that may be more useful: the “sine function” written as sin(x), and the “cosine function” written as cos(x). Before we explain those functions, some additional terminology is needed. Sides and angles that touch are described as adjacent. Every side has two adjacent angles. Sides and angles that don’t touch are described as opposite. For a right triangle, the side opposite to the right angle is called the hypotenuse (from Greek for “stretching under”). The two remaining sides are called legs.

Usually we are interested (as in the example above) in an angle other than the right angle. What we called “rise” in the above example is taken as length of the opposite leg to the angle of interest; likewise, the “run” is taken as the length of the adjacent leg. When applied to an angle measure, the three trigonometric functions produce the various combinations of ratios of side lengths.

In other words:

·   The tangent of angle A = the length of the opposite side divided by the length of the adjacent side

·   The sine of angle A = the length of the opposite side divided by the length of the hypotenuse

·   The cosine of angle A = the length of the adjacent side divided by the length of the hypotenuse

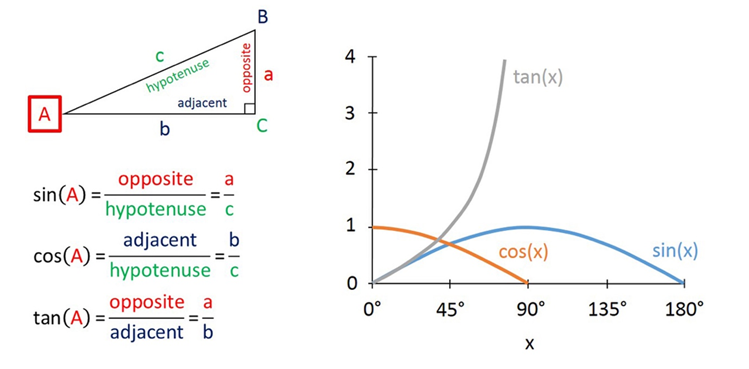
From our ship-mast example before, the relationship between an angle and its tangent can be determined from its graph, shown below. The graphs of sine and cosine are included as well.

下为三张三角函数公式表：

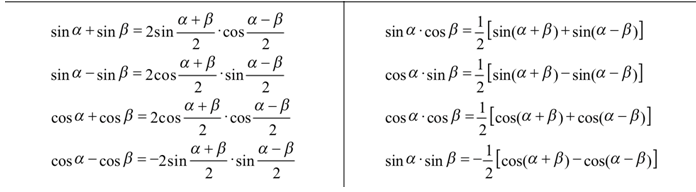
Alevel数学三角函数公式表1

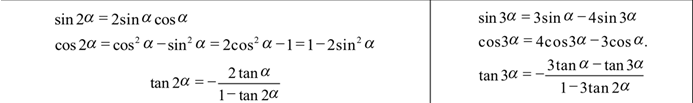
Alevel数学三角函数公式表2

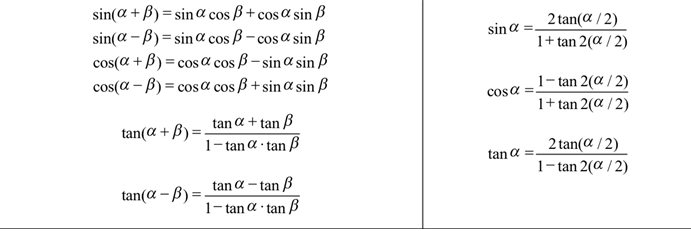
Alevel数学三角函数公式表3

 

上述就是今天介绍的主要内容，如果对此内容有疑问，欢迎在线咨询我们的课程顾问老师，A+国际教育中心是国内领先的国际课程辅导机构，专注于为中小龄学员提供国际课程辅导，包括ks1-ks3、GCSE、IGCSE/Pre-A、A-Level、AP、IB等课程学科辅导，同时为申请英美澳加等国家私立初高中的学生提供入学考试辅导，帮助学生顺利入读国外优秀私立学校。目前在北京、英国、美国分别设有授课中心。